Finally I'm sort of back, and I think I'll resume regular blogging here and in the other blogs very shortly. Thank you to anyone who was actually still waiting around for me to come back!
Famously it has been said that people who like sausage and legislation should not see how they are made. The same might be said of computer simulation modeling, even or especially when it is done to write science fiction stories. But we have ground to cover today, so point the nose right over there where you see all those cowardly angels tiptoeing around nervously, and floor it ...
First of all, my apologies for the long delay here;
something important that I can't quite talk about yet jumped into my life, and
took over for a while. Then
something important, which I also can't talk about yet, jumped in right after that.
I'm excavating as quickly as I can. This site will once again bustle – just not, maybe, right
away.
Father Lucifer and The Book Doctor's
Little Black Bag are likewise on hiatus while the chaos settles, but
something will be coming along in both of them presently as well.
Now, before my unseemly departure, I was talking
about why I am building a simple spreadsheet model of a future with extensive
carbon sequestration (in Part
I, where those of you who are only interested in global warming as a
controversy will probably find out that I have no intention of being useful to
either side), and what I need and want in a computer simulation model I intend
to use for fiction (in Part
II, which may be of more interest to fiction writers and readers than to
anyone else, but this piece might make more sense if you look over the criteria
outlined there).
So here in Part III, let's put our heads under the
hood, dirty our hands, bark our knuckles, and say bad words in front of our
inner eight-year-old who is standing there holding a wrench for us.
This time the problem is working through how, in
actual numbers-on-the-sheet practice, we go about meeting those criteria from
Part II, constrained by the semi-crappy data and theory described in Part I.
There's a logical order to embedding the criteria
for a good fiction-building model into the work:
Simplicity/hackability and rigor are a matter of craft in the building – you just keep them in mind at
every step as you go, and eventually, if you were careful and thorough, it
turns out the whole model is simple, hackable, and rigorous.
Surprise* happens as an emergent property from rigor and simplicity, at least
that's always been my experience.
Build a simple model from well-chosen premises, and it will have be able
to surprise me and force me to imagine things that may initially be hard to
picture, territory where other people have not been yet.
Progression tends to derive from simplicity. Whenever a model I have built has become too complicated, it
has almost always also been too predictable, probably because, as Anatole
France pointed out, "In history it is generally the inevitable which
happens." Each additional feedback loop is another constraint on what the
model can do and what fictional territory it can go into, or to say the same
thing in France's terms, each feedback loop is another rope of inevitability
wrapped around our future history.
Feedback loops cause negative feedback – which is the good kind**,
despite some people's linguistic laziness –and the more complex the model, the
more feedback loops, and therefore the more homeostasis and the more
overdetermination.***
So simplicity, rigor, surprise, and progression
will come up during the nitty-gritty phase of constructing and evaluating the
model.
That leaves two things that need to be designed into the model from the beginning: tragedy and consistency (both with physical reality and within the
story). They're naturally
intertwined. Consistency allows
the reader to feel that the fictional world is real. They will judge fictional reality by the world they know.
Conveniently, that's some subset of our real world, and our real world
conspicuously has many limits.
Our real world is tragic, at least for individuals
in any time that's meaningful within one lifetime. The total effect of all the limitations is always tragic:
everybody dies, nobody spends as much time as they would like on the things
that their best judgment says are important, even the happiest people are
forced by circumstances to waste some big part of their brief lifespans on
things that don't matter to them, and we are constantly forced to make choices
between values we hold as good. As
Dr. Frank-N-Furter so wisely says, "It isn't easy to have a good
time. Even smiling makes my face
hurt."
Consistency leads to limits. For example, "okay, we could have
a super-hurricane, but what's the limit of its superness?" (That led me to
the critical role of the biased random trajectory of stormtracks, surface
seawater temperatures, and outflow jets, in Mother of Storms, whose upcoming
reprint I am flogging relentlessly, and which, incidentally, is also available on
Kindle). And that led to a
tragedy: once the superstorm started you couldn't just wait it out or learn to
live with the one you had; the Mother of Storms would have endless daughter storms.
Another example: "Supposing a terraformed
planet needs to be habitable at the earliest possible date, and we cherry-pick
really ready-to-go terraformable planets, how much longer would terraforming
have to go on after the first settlers arrived?" (About 500-1000 years,
hence the many details of still-being-terraformed worlds in the Thousand
Cultures books, and the tendency on most planets for people to go into the
concrete box – it's just not all that nice outside. So tragically the frontier, which should be leavening
society with new ideas derived from new experiences, tends to rapidly become just
like Earth but less convenient, and the frontier reinforces rather than
subverts Earth's dull conformity).
Even for something as silly and trivial as Caesar's
Bicycle, I looked at the
difference bicycles would have made for the distance a Roman legion could cover
in a day and the amount of baggage it could have taken with it–a man on a
bicycle can easily run a horse- or mule-drawn baggage train to death over a
longer distance, if they try to keep up with him, especially since I equipped
them with muskets which demand a lot more baggage than swords (for one thing,
you don't need barrels of swordpowder to make them work). But peditrucks are
lousy freight haulers, and my alt-Romans weren't quite up to mobile steam power
yet.
Hence it's a world that is better-connected and
better informed but can't necessarily do anything about what it knows. A legion can zoom long distances between
supply depots, operate for a day or two a long way from its baggage train, and
communicate and scout much more effectively, but on long campaigns or away from
roads, it doesn't move much faster than it did in our timeline.) And that difficulty is the kind of
thing I mean by tragedy—it led to several plot points where things turned out
bad for the good people – they could know something was happening but couldn't
get there in time to do anything about it.
So where can we find tragedy and consistency in
carbon in the atmosphere?
This time out I started from some basic
bookkeeping:
According to the ice-bubble studies and a variety
of other confirming evidence, it looks like as late as 1800 there were about 280 parts per million
(in volume) of carbon dioxide in the air.
By the first recognizably modern and careful analyses in 1832, there
were about 284 ppm, and today there are about 392 parts per million.****
To the extent that they all concede that global
temperature can be measured going back more than a couple of decades, most
sources seem to be willing to say it went up about 0.7° Celsius between 1906
and 2005, i.e. across one century (the only one we really know crap
about). Thermometer measurements
become abundant enough back in the 1850s to give us a wholly inadequate idea of
what things were like in some parts of the world. There was a big upward trend in carbon fuels consumption
beginning in the 1840s, not a one-time or permanent increase so much as carbon
fuel consumption going up in a steeper slope; the slope steepened again
1890-1930, and not only steepened but started to bend upward, after 1950. From about 1985 to 2000 there's an
almost-no-questions rapid global temperature increase, and from about 2000 to the present it's
pretty clearly not going down but might not be going up (and is definitely not
going up as fast as it used to).
Most of the slopes, increases, decreases etc. are known with 1-2 digit
accuracy at best.*****
Now, "1-2 digit accuracy at best" means
that when we say "2% increase", there's a big chance it could really
be 1% or 3%, and at least some chance that it's maybe 0.8%, or that 3.6%
wouldn't be wrong. Since doubling
time in periods = roughly 69.3/(pct increase per period), if the number of
zombies (that would be in some other book's model) was 100 today, and we think
there's a roughly 2% daily increase, at one-digit accuracy, we know that there
will eventually be 200 zombies, but since the real rate might be as high as 3%
or as low as 1%, we don't know if that will be in one month or three. That makes a big difference in our
choice to loot Wal-Mart now or wait for Parcel Post to bring the new
shotgun. (All right, if you want
to be all stodgy, it's the same math that applies to things like mortgages and
money market certificates, too.)
Now, a computer simulation model (or
"model" as I call it)******
has two basic components: a system state at more than one specified
time, and a transformation rule. A
system state is just a set of numbers for a set of variables, such as "In
1833 [that's a specified time],
there were 284 parts per million of carbon dioxide in the air, which meant
there were about
620,000,000,000,000 kilograms of carbon in Earth's atmosphere. People burned about 57,900,000 tonnes
of carbon. 7.69 million square
kilometers of land were raising crops worldwide, 2,940,000 hectares of new land
were cleared for farming, 297,000 hectares were cleared to create new modern
urban area, and the interpolated historical temperature rise above the global
temperature of 1800 was just under three-thousandths of a degree Celsius."
You can express that as a row in a spreadsheet; I've shown system states for
1833, 1883, 1933, and 1983, but in my actual model on my spreadsheet I have one
for every year up to 2011 (and a partial system state for 1832, since change
from previous year is an important term).
Year
|
CO2
PPM |
Mass of
carbon in atmosphere, kg |
Carbon burned
by people |
Global
Cropland, square km |
Wild land
cleared for new farmland in Hectares |
Modern urban
expansion in Hectares |
Temp Rise,
Historical Interpolated, °C above 1800 level |
|
1833
|
284
|
6.20E+14
|
5.79E+07
|
7.69E+06
|
2.94E+06
|
2.97E+05
|
0.0029
|
|
1883
|
296
|
6.46E+14
|
2.89E+08
|
1.03E+07
|
7.08E+06
|
6.36E+05
|
0.153
|
|
1932
|
309
|
6.73E+14
|
1.25E+09
|
1.43E+07
|
7.01E+06
|
1.28E+06
|
0.309
|
|
1983
|
343
|
7.47E+14
|
4.57E+09
|
1.79E+07
|
8.99E+05
|
7.44E+06
|
0.729
|
|
Now, some of you may be aware that neither John Quincy Adams nor Andrew
Jackson commissioned a lot of carbon studies, Sir Robert Peel did not include
satellite photos of the growth of London in his reports to William IV, and the
Daoguong Emperor wasn't getting
annual reports on rises in global temperature. So where do these numbers come from?
Mostly they're interpolations between the estimates
prepared by other people for other purposes. Some historian or statistician takes results from local
censuses and land records, from business records of companies that sold coal or
oil, from whatever government statistical studies there were, and from the wild
ass guesses of colonial administrators, and comes up with some rough figures
for, for example, 1881 and 1890.
The modeler, however, wants to work at a more detailed level – say,
annually. So the modeler
calculates values for 1882, 1883, … 1889.
There are a lot of ways of doing this but the two
that are most common are arithmetic/straight-line and
geometric/exponential. In
arithmetic interpolation, you divide the difference between the big units (for
which you have values) evenly into the number of increments between you want to
fill in; in geometric interpolation, you find a growth (or shrink) rate for the
small units that would account for the big change cumulatively. Arithmetic interpolation draws straight
lines on graphs; geometric interpolation draws curves with most of the change
allocated around one of the data points.
Which to use is almost entirely a modeler's
decision, but I tend to be guided by four general principles of craft:
1. where there are several data points along a
curve, if it looks more like a straight line, I use arithmetic interpolation
between those points, and if it curves up or down I use exponentiation,
2. if the line or curve looks smooth between the
big (observed) intervals I fit a line to the whole curve, and if the curve
looks lumpy I interpolate separately between data points
3. if I have good reason to think the underlying
process is exponential (e.g. population growth, monetary inflation, spread of a
disease) I use an exponential interpolation regardless of what the curve looks
like.
4. if I have a good reason to think a function is
linear (e.g. the size of a navy where ships last a long time and shipyards
build at about the same rate all the time), then I use arithmetic
interpolation.
There are two other kinds of interpolation I use
occasionally, asymptotic and
harmonic, but they don't come up in this model, and you're probably already
sleepy enough.
So here are the graphs over time of the
interpolated values for that basic data.
The little source-slug beneath is supplied as an act of pure sadism, so
that idiotic undergrads working on papers at the last minute, desperately
looking for any old graph to prove their point, will impale themselves for
their professors' amusement.
 |
| Source: Frodd, Iyama. "Graphical dysemiosis of global warming data." Journal of Mendacious Prevarication 41 (2013): 7. |
 |
| Source: Frodd, Iyama. "Graphical dysemiosis of global warming data." Journal of Mendacious Prevarication 41 (2013): 7. |
The mass of carbon in the atmosphere graph shows
that variable from zero to a little bit above its current level. If I were trying to propagandize you
here, instead of in my book later, I would either make it look like there was
nothing to worry about by choosing the axes and their intersection point to
look like the line was not coming up much and was still in the middle of the
graph (as in the first), or if I wanted to scare the crap out of you, I would
choose the second arrangement to make it look like an explosion. I haven't decided what mixture of
emotions I want to arouse yet, and I'm the main audience for this thing, so I'm
using relatively honest graphs instead.
This next graph should convince you that the
industrial revolution happened:
 |
| Source: Phuled, Yu Bin. "Historical data on industrial activity from sparse and inadequate sources." Quarterly Journal of Insignificant Correlations21 (1910): 7. |
And this one shows that at the same time large
parts of North America, South America, Australia, and Central Asia came under the
plow:
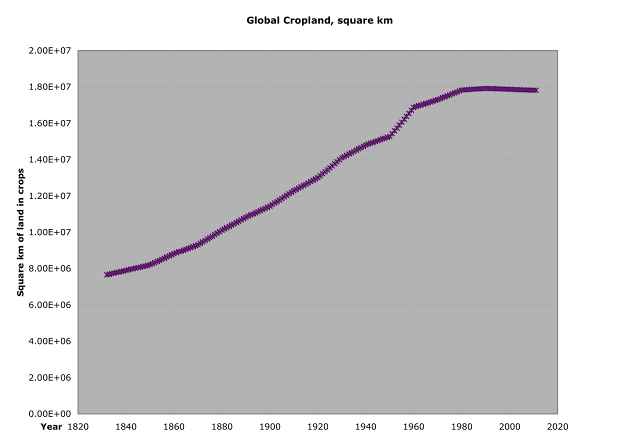 |
| Source: Phuled, Yu Bin. "Historical data on industrial activity from sparse and inadequate sources." Quarterly Journal of Insignificant Correlations 21 (1910): 7. |
Which is especially clear if instead of looking at
total farmland you look at just the new land being cleared each year:
 |
| Source: Phuled, Yu Bin. "Historical data on industrial activity from sparse and inadequate sources." Quarterly Journal of Insignificant Correlations 21 (1910): 7. |
If this were a more critical part of the model I
might think about doing harmonic interpolation – a boom and bust cycle,
indicating that agricultural settlement came in surges. There are quite a few
historical correlations of interest in here, which you can dig out if you're
into that, but I'm rushing on to show you more startling news: the population
grew and moved rapidly into the modern parts of cities ("modern looking" is basically "state of the art" -- parts of the city that had cobblestones, sewers, and gaslights in 1870, electric lights, running water, and trolleys in 1900, telephones and blacktop in 1920, on up to high speed high bandwidth lines today. It's surprising how slowly the "modern" version of city life spreads (there were still some dirt streets in Manhattan in the 1930s), but once modernized it tends to stay up with modern from then on.
 |
Source: Bohgice, Utter Lee. "Odd looking curves
from small amounts of data."
Journal of Vertical Inflection 17 (Summer 2008): 7. |
And now the graph we've all been waiting for. This is the point where some of the few remaining
righties will stalk out in a huff, because I'm using Hansen's NASA numbers and
just extending them where needed.
But, frankly, having read through his methodology, he pretty much did
what I would do or what any analyst would do given the crappy, inadequate data.
You may fairly complain that Hansen's public tone has gotten unpleasant, but
when you do a job this big on data this sketchy, you are going to be vulnerable
to many accusations, and then when so many of the attacks are overwhelmingly
blunt that their true objection is that you failed to get the numbers they wanted, my guess is
that can make a person irritable; it's like being the mess hall cook at Camp
Helicopter Parent.
To extend the graph, I did some testing around, and
basically prior to about 1895, the numbers are indistinguishable from random –
no trend at all – and then they oscillate without any clear direction till
about 1925. So I took the 19th century average to one digit of accuracy, and
called it as good as it was going to get.
Figures weren't there yet for 2010 and 2011 at the site I found, but
since (as the righties have been vaunting for a while) temperature change has
slowed down, I just set them to the 2000s decade average as well.
 |
Source: Lyer, B.F. "Global temperatures for the
irritation of talk-radio fans." Review of Lumpy Graphs 17(2022):
7.
|
Such, then, are the system states -- the descriptions of the way things were at each year.
The other part of the model is the transformation
rules – in fact that's what makes it a model rather than just a database of a
lot of made-up data. A transformation rule takes the values from a previous system state or states and uses them to calculate the next.
In my very
simple model, all the added carbon in the atmosphere is coming from human
beings (yes, I can hear the anti-warmers exclaiming AHA! So it was made to
be that way, and they're right,
again, this is about writing a novel, not about solving the world).
Furthermore, I only count four big human activities putting carbon into the
atmosphere (Grossly inadequate,
the actual climate scientists mutter, and they too are right):
1) burning it (including roasting limestone to make cement),
2)
clearing wild land to turn into cropland (a one-time thing because after the
wild land's roots are dug up and the brush burned, the net effect of the crops
is fixing carbon rather than releasing it,
3) clearing wild land or cropland
for urban environment, and
4) general living in modern urban areas.
For each of these processes, there are
some reasonable middle of the road figures for how much carbon they release into the air, and for how much of each activity there was going back in time, again, all figures from that least imaginative of all sources, Wikipedia articles where there wasn't much complaint in the talk or discussion sections.
But we can also figure the increase in carbon directly from the
changes in the amount in the air. So for each year, there's how much people put
in, and how much carbon the atmosphere gained. Graphing human input versus net gain against each other, we have this:
That arrow labeled "perfect correspondence" is where the
graph would be if every single bit of added carbon in the atmosphere were put there
by people, and every bit that went in stayed there -- a straight line through the diagonals of the boxes, a 45°
line if the scales are the same.
Reassuringly (at least for the sake of the model), it looks like when we
put in a bit over 10 billion tonnes of carbon, only a bit over 4 billion hang
around so the data points almost all fall below the perfect correspondence arrow. If large natural sources (volcanoes,
forest fires, methane releases from permafrost or the seabed, the Carbon Fairy
going off her meds) were the most important, the data points would lie mostly above the arrow.
So the thing to be explained and modeled is not where the carbon is coming from – there's more than enough from known human
activities – but where the carbon we put into the air is going, i.e. why don't we get all the carbon in the air
that we pay to put there. (Maybe the Carbon Fairy, like the Tooth Fairy, is
taking our carbon away and leaving us quarters, in which case I would like to
know why I never got my quarters.)
That other close-to-six-billion tonnes must be presumed to be going into the various
"sinks" – dissolution in the ocean, absorption in soil, consumption
by rain forests and plankton, coral reefs, fish crap sinking into bottom mud
and being run over by drifting continents, being compressed into Coca Cola,
being used to make Styrofoam that is then buried, whatever. (These are not necessarily all the same
sized effects). For the model, we want some idea about how the sinks behave for
different levels of actual CO2 (common sense and the law of partial pressures
would say that the more CO2 there is in the atmosphere, the more will go into
the sink) and cropland (cropland is known to be a good sink, so the more there
is, the faster the sink should run).
Metaphorically, how much goes out the drain depends on how high the
pressure is (i.e. how much is piled up on top of it) and how wide the drain is.
Here are those graphs:
Notice that because carbon goes up pretty steadily, it acts as a kind of clock in these graphs; the horizontal axis is not proportional to time but it is in pretty much the same order, with most of the points to the left being back in the nineteenth century, those in the middle being the middle of the twentieth century, and those to the right being mostly in the 21st.
What jumps out is that there's a definite association with both total
carbon and cropland, but that as the amount of cropland has reached a maximum
and stuck there (you just can't cultivate the Sahara or Himalayas, let alone
sodbust on Antarctic ice or the surface of the Pacific), the partial pressure
becomes more of a factor in the sinks, and the expansion of cropland less.
So thus far we've got a model that works not-too-badly to one digit of
accuracy – and by not-too-badly I mean that it supports the following
interpretations, which fit pretty well with what seems to be true:
• most of the carbon increase is people
• the amount that stays in the air is comparable to the amount that
goes into sinks,
• how much goes into the sink depends partly on how much is in the air
pushing it into the sink
• how much goes into the sink depends partly on how much cropland
there is absorbing it, but we won't be expanding cropland much (based on the
last few decades).
Now for the big issue: that linkage to temperature. For problems like this, I believe it's
always worthwhile to do some very simple graphic tests just to see if the basic
idea of the model is plausible, and in this case I'm simply normalizing added
atmospheric carbon and increased temperature between their minima and maxima,
which puts them into a common 0-1 scale, and putting them on the same
graph. If you're not familiar with
normalization, here's another
place where I explained it to another audience. The result is actually rather striking:
The carbon-to-temperature linkage is much more convincing after 1950
than before, but since I'm writing about the future, that's where I want it to
be convincing. This is also
interesting because
1. it's the period when data on both carbon releases
and temperatures begins to be much more reliably and accurately measured.
2. it's the period when there's a sudden sharp upward
inflection in total area of modern cities (see graph above) –
"modern" meaning state of the art, but after 1950 that means paved,
built up, with a full set of pipes and wires, cars running in the streets,
etc., and it's also a period when new city land is mostly coming at the expense
of effective carbon sinks like agricultural land, forests, and especially
estuaries and other wetlands.
3. there's also a sudden sharp upward inflection
(graph above) in land under cultivation, at least 1950-80. That was due to
several factors – the Green Revolution which made much more land economic to
farm, the Soviet New Lands program
(the one that drank the Aral Sea), the Chinese, Brazilian, Indian, and other
self-sufficiency drives, and the last big wave of dam building in the
American/Canadian West. Again,
remember that cultivated land is a carbon sink, but getting wild land into
cultivation is a carbon source.
Another way to look at this is via a Normalized Median Graph (if you'd
like more explanation, see the same All
Analytics article). With a
Normalized Median Graph, the more points that fall into the low-low (lower
left) and high-high (upper right) quadrants, the stronger the correlation; the
more that fall into the other quadrants, the less strong the correlation (and
the more likely it is to be purely random). As you can see, there is quite a strong correlation;
practically all the points fall into the low-low and high-high boxes:
Again, because left-right order and bottom-top order are roughly but
not exactly chronological, it should be apparent that the earlier points are in
fact bunched around the origin (indicating a steady state without much change)
and that most of the correlation is coming from the later points (which flow
overwhelmingly into the 4th (hi-hi) quadrant). Nonetheless even that bunch around the origin is distinctly
scattered mostly into the low-low, high-high. At least superficially the model of anthropogenic
atmospheric carbon driving global warming is holding up pretty well here; if I
had a graph like that in a marketing study, I'd tell the client to bet some
money on it.
I'd also tell the client to commission more studies, by the way,
because although this does show a relationship, it might be entirely
specious. When you have two
mostly-rising variables, they will always correlate to some extent, and may
correlate strongly, not because they are causally related but because the math
of it says that two lines with consistent (though different) average slopes are
going to have a linear transform between them. A scatter that fell evenly across all four quadrants would
have been enough to strongly suggest that there wasn't much correlation, but it doesn't work the other way -- a
scatter that falls heavily on one diagonal does not prove a correlation.******* So all we've shown here is plausibility, but hey, I'm writing fiction, and that's all I need.
One very possible speculation that emerges from the improvement in correlation after 1950: up through WW2 we were insulated from our
bad carbon habits by the immense size of the sinks – visualize it as a bathroom
sink with a huge, far more than needed free-running drain, while we fairly
slowly open the faucet. At first,
the water only accumulates a little bit faster, just because there's a slight
time lag between water coming in and going down the drain. But then the drain clogs somewhat, and
we lose the cushion of the extra big drain. At that point the depth of water in the sink is
responding much more strongly to what the faucet does, and if we then also open
the faucet wider, things get much worse much faster, and we have much less time
to correct things before the kitchen floor is flooding.
This is where I write a huge note to myself: remember the whole
purpose of this huge document is that I want to do a story about carbon
sequestration. Maybe the reason
humanity finds it has to do large scale sequestration is the discovery that
whatever the case might have been before, we have now clogged the drain, and
thus we need to either actively dig out the clogs, or perhaps cut a new
drain. Maybe, in other words, it
starts to get much worse much faster, and it's sequester or else.
Or else what? We'll
consider that over in Part IV, which we can hope won't get backed up behind as
much other, more critical work as this part did. There are clogs everywhere once you start to look.
Meanwhile, let's finish that model:
Having seen a pattern that at least makes sense internally, it's time
to look at whether I can achieve any consistency with the external world. I'm going to use the generally accepted
figure for estimated radiative forcing of the current elevated level of CO2,
which is 1.66 watts per meter squared.
Radiative forcing is in units of energy per time-area and it measures additional heat
retention over what would be retained by a pristine atmosphere. So what that number means is that in
any given second, a meter of the Earth's surface will retain 1.66 more joules
of sunlight energy than it did in 1750 or so. (1 watt=1 joule per second). Now, conveniently, things work out because although how much
sunlight falls on any square meter of the Earth's surface at any given time is
a complicated business that requires trigonometry, the total receiving
area is always the same: that
of a disk with the diameter of the Earth.
We know how many seconds there are in a year, that area, and that
radiative forcing, and multiplying them together we get the additional heat
energy that the Earth hangs onto now.
Furthermore, since radiative forcing is defined relative to the
pre-industrial baseline, and is known to be directly proportional to carbon
content, then from either PPM or tonnes of atmospheric carbon, we can calculate
it for every previous year (from those highly suspicious interpolated values,
but again, remember, this aims at plausible fiction, not at solving a problem
that vexes real scientists with actual computers and instruments). And since we know the specific heat of
air (out of which the atmosphere is very conveniently made) we can calculate
how much temperature rise the Earth's atmosphere would have had if all that
heat were retained.
But of course it wasn't; some heat went into rocks and the ocean and
some radiated back into space. So
we expect the actual temperature rise to be below the temperature rise
calculated from retained heat, but related to it. Here's what that graph shows:
The black, dashed diagonal line would represent
perfect prediction, which is not
what we're looking at here at all.
There's a lot of veering wildly around in the lower part of the graph
(the early 19th century when data are lousy and perhaps when more sinks are
available), but then after that it settles into a rhythm where the lines run
parallel, with some "mystery sink" or other carrying off much of the
heat, and then every so often there's a brief depression in the actual line
that is always quickly caught up.
This observation is not heartening as to the
present flattening of the "actual" curve; it suggests that the system
may be quite capable of making up the difference suddenly, sometime in the next
decade. In fact, at a guess based
on a little bit of eyeballing that I didn't pursue much farther, gaps tend to
open up between predicted and actual, with actual being colder, during solar
minima, and close during solar maxima.
So one possible effect might be that carbon in the atmosphere changes
the responsiveness
(click the link for a spiffy explanation of responsiveness, by me) of atmospheric temperature to the solar cycle; the more carbon, the more that a
small twitch of the sun triggers a big change in temperature. If so, our climate problem could
actually be a good deal worse, with both steeper, deeper plunges and faster,
higher climbs – harder for wildlife and agriculture to adapt to, more apt to
bring on harsh weather, and much more destabilizing in the fuel and food
markets. (And to paraphrase Trotsky, whether or not you are interested in the
fuel and food markets, they are interested in you).
Once again, as soon as the data gets decent, the
pattern becomes clearer. That is
another reason why, although I acknowledge that many nits remain to be picked,
I think on balance we have to behave as if we were sure that our activities
were warming the planet. If better
data resulted in more ambiguity or the disappearance of the claimed effect, I'd
be more in sympathy with the skeptics, but the situation is the opposite of
that.
So how big is the heat sink? For the 1950 to 2000 period
that has the best data, an overall average of about 16.5% of the heat that
the gases should have captured went somewhere else (radiated to space, soaked
up in oceans or soil, the Heat Fairy carried it off. Do you suppose the Heat Fairy might be dating the Carbon
Fairy? Aren't you glad there's no comments area so nobody can now make a pun about carbon dating?).
In the 1950-60 period the mystery heat sink was
claiming about 22% on average; in 1985-2000 that fell precipitately to about
6%, and has been rising slowly again since. This suggests that the Mystery Heat Sink is subject to
whims, which may be very important for the story -- it's another place where things could go wrong and get bad quickly.
So at this point, we've got a nice simple model
that bears some resemblance to consensus reality, and laid out as an arrow
diagram it looks something like this:
Arrows labeled with + are sources and/or positive
feedbacks (places where heat or carbon comes from, and where more causes
more) and those with – are sinks
and/or negative feedbacks (places where heat or carbon goes, and where more
causes less.)
And with that model in place, if we have some kind
of figures for how much carbon people can be expected to burn (projecting off
population and various energy-efficiency issues), how many will live in cities,
and changes of land use … we've got a model that can now be run forward into
the future to "predict" temperature changes. BIG quotes around predict.
Furthermore, by adding other sinks – that's what
sequestration is – we can see what differences might be made, and look for
reasons why people might want to make them (or try to make them), and with what
consequences (expected and not).
So in Part IV we'll generate a variety of
carbon/heat futures with a varied mix of carbon restriction and carbon
sequestration, and see which one might make a better story … but for now, as
you may have noticed, this part has already run rather long.
See you whenever the chaos lifts again.
=================================
*For example, the model underlying the forthcoming Losers
in Space looked at "what
fraction of people are needed for jobs that, when done by people, are either
more fun (like athletics or entertainment), or just feel better for the
consumer (like kindergarten teaching or nursing)?" From the assumption
that strong market pressure to automate all jobs everywhere except the
un-automatable continues through the next 110 years, with technical capability
per cost increasing at reasonable pace, the result turned out to be that within
70 years, you have a bit less than 4% of the adult population with jobs, and
96% of adults permanently on the dole, with work a rare privilege, and that
shapes the whole world, leading to questions like what does everyone do all
life? (Lots and lots of things,
some wonderful, some horrible, most just things). How does life feel when most
people only know a few people who have ever worked? (After a generation it's
like any other thing once common that has become rare – long trips by
horseback, being press-ganged into ten years service on a Navy ship, taking
exams entirely in Greek or Latin, extracting a cube root manually). Especially since the calculated social
minimum turns out to be the equivalent of about $300k per year in 2010 dollars,
with many things widely available cheaply that don't exist at all today. (Some dole!)
**Negative feedback: in any cyclic process, the signal at some point
that says the more there is, the less will be added, e.g.:
Thermostats.
Insulin cycles in people who are not diabetic.
Handshake pressure by polite people
Predator prey cycles.
Neutrons in normally functioning nuclear reactors.
Democratic resistance to oppression.
Positive feedback: in any cyclic process, the signal at some point
that says the more there is, the more will be added.
Neutrons in atom bombs.
Population explosions.
Panicked drivers standing on the brake in a skid.
Epidemics.
Witch hunts.
Bullying.
Arms races.
Terrorism.
Remember all this the next time someone offers to
give you some positive feedback; just cackle maniacally and shout "Soon
all the world shall be mine, and every ignorant fool will pay!"
***For us of the Mathundstatz Tribe a quick
reminder (and for those not of the tribe, a probably-inadequate explanation):
although overdetermination and underdetermination have a more generalized and
complex meaning, they're easiest to grok if you think about a system of linear
equations, one of those things you learned to solve in middle school or
so. If you have fewer equations
than variables, you are underdetermined, which means that there are an infinite
number of solutions (which must follow some rules, so not everything works, but
there are an infinite number of things that do. A typical solution set (i.e.
the set of all the answers that work) for an underdetermined system might be
"the even positive integers," (2, 4, 6 …) which is infinite, even
though there are also many other infinite sets of answers like –2, 1/2, π, and
927 that are excluded).
Overdetermination is the opposite – too many
equations and not enough variables – so there is never an exact solution, but
there are better and worse approximations (for example, if we have
x+2=4, and
3x=7
i.e.
one variable and 2 equations, the system is overdetermined, but if we answer
with x=2.3, that minimizes the sum of the squared errors, so 2.3 is a
"better" answer than, for example, x=1.9 or x=2.84. The process you learn in second-term
stats called "multilinear regression" is simply a process for finding
the answer to a much more complicated version of that, in which there might be
dozens of variables and thousands of equations.
There is an excellent argument, by which I mean one
that convinces me, that the real social world is overdetermined – that if you
wrote accurate predictive equations for everything that happens in human
culture, you would discover that they could not all be satisfied, so because
there has to be something, the
social universe wobbles around among "pretty good" but somewhat
inconsistent results, and that this actually explains why so many things seem
to be constantly changing without apparent cause.
So for our fictional world to feel real, it needs
to be a little overdetermined – but if it is too overdetermined, it's Anatole
France's world, where, for example, the American Civil War was bound to happen
because of slavery, tariffs, states rights, cultural changes, religious
differences, etc. and any of those is enough to explain it; "the
inevitable happens" because of overdetermination. There's a Goldilocks zone of slight
overdetermination that I aim for, and with much practice, can eventually find
my way to.
**** A moment for numeric contemplation: How small
is 280, or 392, parts per million?
Imagine a square of quarter inch quadrille, that
not-too-dense graph paper a lot of us use for drawing projects, which is 1000
squares on a side. That will be
twenty feet ten inches on a side
(a bit bigger than the floor area of a smallish studio apartment or a
two-car garage). You color an area
of 14x20 squares (that's an index card—3.5x5 in) . That's the original amount of CO2 relative to the atmosphere
of that that floor-sized sheet.
The additional CO2 from human beings is about 110, or a ten-by-eleven
rectangle (2.5" x 2.75" – smaller than a standard playing card). You're looking at why some people with
good number sense have a hard time seeing how a little change in a little
number can make such a big difference.
But it can.
Visualize a stage counterweight system with the brake off, and a
convenient lack of friction. You
have a one-tonne batten (that pipe they hang lights and scenery from) hanging
in balance with one tonne on the arbor (those racks that hold counterweights),
and since a tonne is a million grams, suppose you're playing with a difference
of 280 PPM – imagine one of those counterweights on the arbor is 280 grams (or
ten ounces). With the batten at
the top, sixty feet above the stage, you take off that weight, so the batten
will start to fall slowly to the bottom; in a bit over half a minute, it will
hit with a force equivalent to a smallish car going at about 1/5 mph, enough to
dent your door in the parking lot or break your knee or collarbone.. Conversely, with the batten at the
bottom and the arbor at the top, and in balance, add a 112-gram counterweight
(4 ounces). 55 seconds later that
1-tonne batten will sock upward into the grid at 1/7 mph – enough force to
knock you down with a good-sized bruise.
The problem with those tiny amounts is that quite literally, they add
up and they leverage.
*****All those global warming figures, and many
more to come, by the way, come from hopping around in Wikipedia and checking
sources to avoid the more obvious advocates, deniers, and loons, exploiting
what Wikipedia does best: going right down the middle of the road in a very
fact-heavy kind of way. That's not
necessarily the way anybody else would go, but it has the virtue of not having
to adjudicate too many competing claims, and again, I'm not trying to make
policy, I'm trying to write a future most people can believe is plausible.
****** At various points in this blog I have used
the words "raw," "naked," "brutal," and of course
"fucking," and since I began this series I am now frequently saying
"model." Visitors are coming in daily on some combination of those
search words, not finding any "raw naked brutal fucking of models,"
and presumably leaving almost immediately. Although anyone searching for "infuriated by her
anything-but-model husband's brutal discourtesy, she said he could eat his
meatloaf fucking raw" is probably disappointed, too.
*******Sorry about that for people who wanted
proof. See Part I again; I'm doing
this to make up a plausible story, not to uncover the truth. That is the job of other people – who
need a ton of funding, much wisdom, and perhaps more careful (as opposed to
aggressive) critical scrutiny, fewer bizarre accusations, and some serious
supporting development in statistics (some of the math they need is not yet
fully developed).






